Imagine that you are at a skatepark, right at the top of a ramp, ready to take that thrilling dive. The higher you are, the more energy you have got stored up, due to gravity. It’s like, when you finally roll down, all that potential energy transforms into kinetic energy—that rush of movement. Now, consider the electric potential difference similarly in electrostatics. Instead of gravity tugging at weights, it’s electric fields that are at play, either pushing or pulling on electric charges. It is a beautiful cool concept, really, how energy changes form like that.

Your height at the skatepark influences how fast your board can go. In the same way, electric potential difference determines how charges zip around in space. So, what exactly is electric potential difference (let’s call it ΔV)? It is basically the work you do to move one unit of charge from one point to another in an electric field. To keep it simple, volts are equal to joules per coulomb.
Now, why should you care about electric potential difference? It is the foundation of so many things in our lives. This includes the batteries that keep our phones running and the circuits in computers. It also encompasses lightning strikes and even the signals that zip through our brains.
If you’re new to ideas like potential difference, a good place to start is Basic Physics: A Self-Teaching Guide — it explains physics in a very easy-to-understand way.
If you understand this idea, you’ll discover how electric fields create the voltage that powers everything around us. Let’s explore this concept.
Formal Derivation from Electrostatics
1. The Line-Integral Relationship
The link between electric fields and potential difference comes from this mathematical tool known as the line integral. Here’s the formula you need to know:
ΔV = -∫[A to B] E⋅dr
This equation tells us that the potential difference between two points, A and B, equals the negative sum (or integral) of the electric field along any path you take from A to B.
What about that negative sign?
It is very important to know that when charges move in the direction of the electric field, they lose potential energy. That’s why the negative sign is taken.
And here is another important idea: E = -∇V.
In static fields, the electric field points to where the potential drops off the quickest.
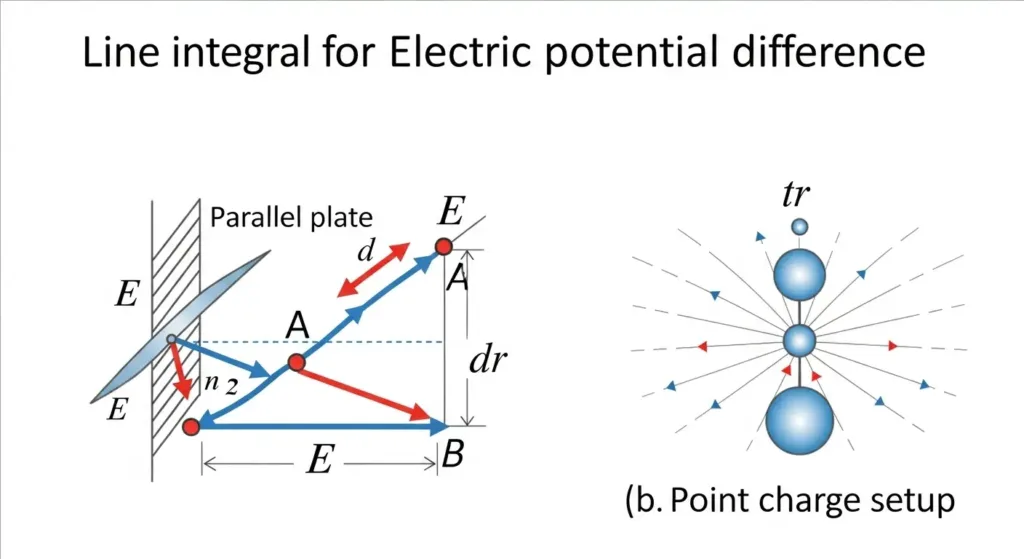
From Simple to Complex Concept
Alright, let’s break it down from simple to complex. Start with a really straightforward case: a uniform electric field between two parallel plates. Here, the electric field (E) is constant, making voltage calculation a breeze:
ΔV = E·d
where d is the distance between the plates. This basic idea pops up in capacitors and a bunch of electronic components. Now, let’s get a bit more complex with a point charge Q. If you are at a distance r away from it, the electric field is given by:
E = kQ/r² (and it is pointing outward).
To figure out the potential difference from way out in space (we can call that infinity) to a distance r:
ΔV = -∫[∞ to r] (kQ/r²) dr = kQ/r
So, there you have it! For point charges, potential difference follows that familiar formula V = kQ/r.
Equipotential Surfaces & Field Mapping
Equipotential surfaces are basically like the shapes where every single point has the same electric potential. It is like those flat contour lines you see on a map—when you move along them, your elevation does not change at all. In the world of electrostatics, you can move a charge along these surfaces without doing any work. Remember, ΔV = 0.
Key Properties of Equipotential Surfaces
- No work is done when moving a charge along an equipotential surface, as (ΔV = 0).
- The electric field is always perpendicular to equipotential surfaces, pointing toward decreasing potential.
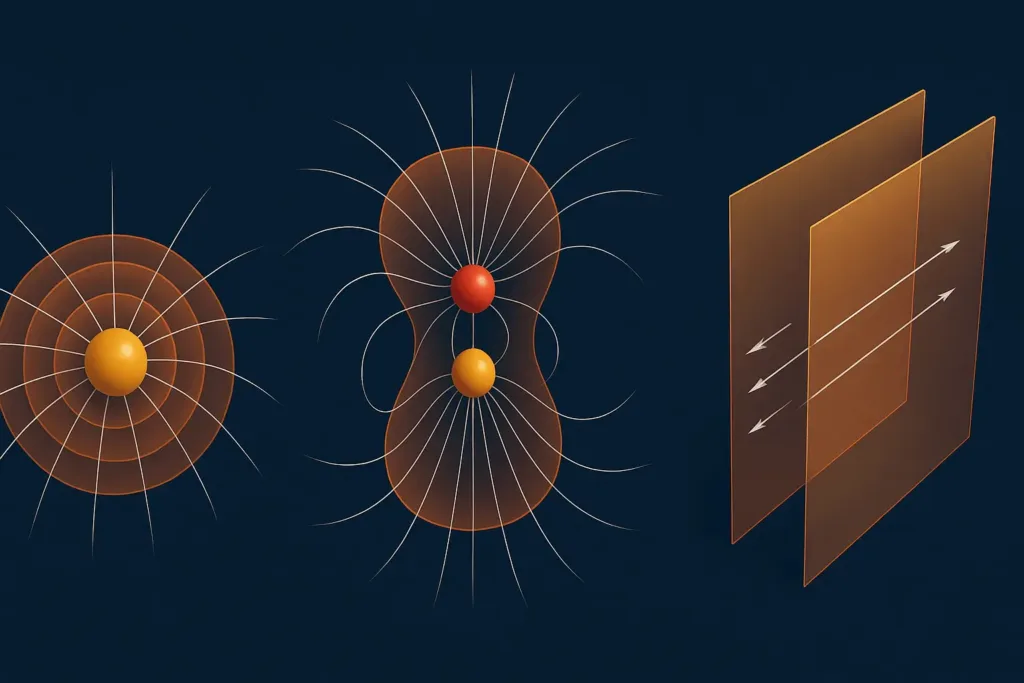
Visual Examples
- Point Charge: Equipotential surfaces are concentric spheres centered on the charge, since (V = kQ/r) depends only on distance. (See Figure 1 for a diagram of concentric equipotential spheres around a point charge.)
- Uniform Field: Equipotential surfaces are parallel planes perpendicular to the field lines, as seen in capacitors.
- Dipole: Equipotential surfaces form complex, distorted shapes reflecting the field’s symmetry between positive and negative charges.
Interactive Challenge
What happens if you slide a positive test charge tangent to a spherical equipotential vs. directly toward the center? Share your answer in the comments.
Real-World Calculation Walkthrough
Alright, let’s dive into some practical examples. These examples show how we can calculate electric potential energy per unit charge in real-life scenarios. It’s a very interesting topic, and honestly, it’s more helpful than you might think!
Problem 1: Uniform Field Calculation
A test charge q = 2×10⁻⁶ C moves 5 cm in a uniform electric field E = 1000 V/m.
Given:
- Charge: q = 2×10⁻⁶ C
- Distance: d = 0.05 m
- Electric field: E = 1000 V/m
Solution:
- ΔV = E·d = 1000 × 0.05 = 50 V
- Work done: W = q·ΔV = (2×10⁻⁶)(50) = 1×10⁻⁴ J
- Energy change: ΔU = W = 1×10⁻⁴ J
Electric Field Strengths and Their Practical Applications
| Electric Field Strength (V/m) | Application/Example | Context |
|---|---|---|
| 0.1–1 | Household electronics | Safe operating levels for consumer devices |
| 100–1,000 | Laboratory experiments | Typical values in physics demonstrations |
| 3,000 | Air breakdown threshold | Where sparks begin to form in dry air |
| 10,000–100,000 | Capacitor plates | Energy storage in electronic circuits |
| 1,000,000 | Electron gun (CRT) | Accelerating electrons in old TV screens |
| 3,000,000 | Lightning bolt | Natural electric discharge in storms |
| 10,000,000 | Medical defibrillator | Life-saving cardiac rhythm correction |
| 1,000,000,000+ | Particle accelerators | Research facilities like CERN’s LHC |
Problem 2: Point Charge from Infinity
Calculate the work needed to bring a charge q = 1×10⁻⁹ C from infinity to a distance r = 0.1 m from a source charge Q = 5×10⁻⁶ C.
Solution using V = kQ/r:
- V(∞) = 0 (by definition)
- V(0.1m) = (9×10⁹)(5×10⁻⁶)/0.1 = 450,000 V
- ΔV = 450,000–0 = 450,000 V
- Work required: W = q·ΔV = (1×10⁻⁹)(450,000) = 4.5×10⁻⁴ J
Practical Applications
These calculations go beyond mere academic exercises. When there are high potential differences between plates, they generate very strong electric fields that are really important for many things like:
- Electron guns in old CRT monitors (thousands of volts)
- Particle accelerators (millions to billions of volts)
- Sensors that detect tiny changes in electric fields
- Medical devices like defibrillators and X-ray machines
Concept Check & Debunking Common Misunderstandings
Let’s talk about the confusion that often trips up students when they are diving into electric potential difference in electrostatics. It is easy to mix things up. You have got these concepts that are related, but they are not quite the same. So, let’s break it down a bit.
1. Critical Distinctions
- Electric Potential (V): The potential energy per unit charge at a specific point. Measured in volts.
- Electric Potential Difference (ΔV): The change in potential between two points. Also measured in volts.
- Electric Potential Energy (U): The total energy a charge has due to its position. Measured in joules (U = qV).
| Concept | Definition & Equation |
|---|---|
| Electric Potential | Definition: Potential at a point compared to a reference (e.g., infinity). Equation: V=kq/r |
| Potential Difference | Definition: Work per unit charge between two points. Equation: ΔV=V2−V1=−∫E⋅dr |
| Potential Energy | Definition: Energy of a charge due to its position in a field. Equation: U=qV |
2. Common Misconceptions Debunked
Misconception 1: “Charges flow along equipotential surfaces”
Reality: Charges flow perpendicular to equipotential surfaces, after electric field lines.
Misconception 2: “Zero potential difference means no electric field”
Reality: Zero ΔV between two specific points doesn’t mean zero field everywhere. The field could be perpendicular to that path.
Misconception 3: “Higher potential always means stronger field”
Reality: Field strength depends on how rapidly potential changes with distance (E = -dV/dr), not just the potential value.
3. Common Beginner Questions & Clarifications
No, if there is an electric field, there must be potential differences between different points.
Because electrostatic fields are conservative – their work done depends only on starting and ending points, not the path taken.
The curl of the field equals zero (∇ × E = 0), meaning no circulation around closed loops.
The field points in the direction of the greatest potential decrease, which is always perpendicular to surfaces of constant potential.
Applications & Future Topics
The study of electric potential difference electrostatics opens doors to multiple applications in modern technology and natural phenomena.
1. Circuit Theory Connections
The potential difference concepts from electrostatics directly translate to:
- Battery voltage: The ΔV a battery maintains between its terminals
- Ohm’s Law: V = IR relates potential difference to current and resistance
- Kirchhoff’s voltage law: The sum of potential differences around any closed loop equals zero
2. Charge Motion in Fields
When charges accelerate through potential differences, they gain kinetic energy equal to their loss in potential energy:
½mv² = qΔV
This principle powers:
- Cathode ray tubes (electrons accelerated by high voltages)
- Mass spectrometers (ions separated by charge-to-mass ratio)
- Lightning (charge buildup creating massive potential differences)
3. Energy Storage Systems
Capacitors store energy by maintaining charges at different potentials: U = ½CV² = ½QΔV
This energy storage principle enables:
- Camera flashes (quick energy release)
- Defibrillators (life-saving electric pulses)
- Power grid stabilization (smoothing voltage fluctuations)
Looking Ahead
Future articles will explore:
- “How Batteries Create and Keep Potential Differences” – The chemistry behind sustained ΔV
- “From Static to Dynamic: When Charges Start Moving” – Transitioning from electrostatics to current electricity
- “Capacitor Design and Energy Density” – Engineering applications of electrostatic principles
Conclusion
So, let’s talk about electric potential difference—it’s a pretty big deal in electrostatics, right? It ties together electric fields, work, and energy in a way that is very important. Think about it: from something as simple as a skatepark to more complex concepts, ΔV really dictates how charges move and keeps a lot of our everyday gadgets running smoothly. Whether you are diving into physics, or you just have a passing interest in electricity, understanding ΔV can help you comprehend circuits. It can also help you grasp batteries and all that good technology.
Challenge For You!
Next time you’re near a charged object (like a balloon rubbed on your hair), imagine the equipotential surfaces around it. How does their spacing show the field’s strength? Try sketching it!
We really want to hear your thoughts! Have you stumbled upon ΔV in your studies or maybe in your everyday life? Feel free to drop your thoughts, questions, or any examples in the comments. We’re all ears!




