Half-Life Calculator & Decay Chain Explained with Examples

Many people feel uneasy when they hear the term nuclear physics. They often think it only deals with atomic bombs, nuclear reactions, and dangerous effects. In reality, nuclear physics is about studying how the tiniest building blocks of matter change over time. One of the most fascinating and practical ideas in this field is half-life. By learning how radioactive decay and how half-life calculator work, we can solve problems in many areas — from nuclear medicine and archaeology to managing nuclear energy. If you’re a student learning nuclear physics or a professional working with medical isotopes, mastering half-life concepts gives you access to exciting applications like carbon dating fossils, creating PET scans, and handling nuclear waste safely.

In this article, we will take you step by step through the half-life formula, will explain decay chains, and show you some solved problems so you can practice on your own. Plus, we have added an interactive half-life calculator — so instead of just memorizing equations, you will actually see how radioactive decay works in real-time.

By the end, you’ll be able to:

• Understand the meaning of half-life in simple words.
• Use the formula to solve physics problems.
• Explore the decay chains like uranium-238 → thorium → lead.
• See some applications in medicine, space exploration, and energy.

Let’s begin by clearing up the basics: what exactly is half-life?

What is Half-Life?

Imagine a box filled with unstable atoms. Each one acts like a tiny ticking clock that eventually goes off by changing into something else. The half-life tells us how long it takes for half of those atoms to decay. You can think of it as a countdown timer that never really reaches zero.

For example, if you start with 100 grams of a radioactive isotope that has a half-life of 10 years, then:

• After 10 years, 50 grams remain.
• After 20 years, 25 grams remain.
• After 30 years, 12.5 grams remain.

The material never fully disappears — it just keeps halving over equal time steps. This steady and predictable pattern is what makes exponential decay so powerful and useful in science.

In simple terms:

Half-life is the time needed for half of a radioactive material to decay.

The Physics Behind Half-Life

Now let’s get a little more formal. The behavior of radioactive materials follows an exponential decay law, which means the rate of decay is proportional to the number of atoms still present.

The mathematical formula is:

N(t) = N₀ e^(-λt)

• N(t) is the number of atoms remaining after time t.
• N₀ is the initial number of atoms.
• e is Euler’s number (approximately 2.718).
• λ (lambda) is the decay constant, which is unique for each isotope.
• t is the elapsed time.

The decay constant (λ) shows the probability of a nucleus decaying per unit of time. A larger lambda means a shorter half-life. This foundational equation is the first step in solving nuclear physics half life problems.

Half-Life Formula Explained

The half-life (T½) and the decay constant (λ) are inversely proportional to each other. A simple derivation connects these two, making it easy to calculate one if you know the other.

Derivation of T½ = 0.693/λ:

We can derive the half-life formula from the exponential decay equation. We know that after one half-life (t=T½), the number of remaining atoms will be half of the initial amount, so N(t)=N₀​/2.

Let’s substitute this into the main formula:

N₀​/2 = N₀ e^(-λt)

Dividing both sides by N₀​:

1​/2 = e^(-λt)

To solve for T½, we take the natural logarithm (ln) of both sides:

ln(1/2) = ln(e^(-λt))

Using the properties of logarithms, ln(1/2)=−ln(2), and ln(e^x)=x, we get:

−ln(2)=−λT½

ln(2)=λT½

T½=ln(2)/λ

Since ln(2)≈0.693, the formula simplifies to:

T½=0.693/λ

This simple formula is extremely powerful. Once you know the decay constant of a substance, you can instantly calculate its half-life. Let’s practice this formula using some examples:

1. Carbon-14 (used in archaeology)

Decay constant: λ≈1.21 × 10^-4 per year

Half life:

T½ = 0.693/1.21 × 10^-4 ≈ 5730 years

This is why archaeologists can date fossils and artifacts up to about 50,000 years old using carbon dating.

2. Uranium-238 (used in geology & reactors)

Decay constant: λ≈4.92×10^−18 per second

Half life:

T½ = 0.693/4.92×10^−18 ≈ 4.5 billion years

This is nearly the same age as the Earth, which makes uranium isotopes perfect for dating rocks.

With this formula in hand, you can now move beyond definitions and actually calculate the lifespan of different isotopes. For deeper insights into these concepts, “Introduction to Nuclear Physics” by Krane provides excellent derivations and additional practice problems.

Half-Life Calculator

Forget complex calculations. Our interactive half-life calculator makes solving these complex problems a breeze. It’s a great radioactive decay calculator for students and enthusiasts alike.

To use the calculator effectively, follow these steps:

1. Enter your initial quantity (atoms, grams, or activity)
2. Input the half-life value with appropriate units (seconds, years, etc.)
3. Specify the elapsed time in matching units
4. Click “Calculate” to see remaining quantity and percentage decayed

The calculator then instantly computes the amount of substance remaining. This is a perfect way to visualize the concept of exponential decay without doing the math by hand.

Radioactive Decay Chains

When a radioactive element decays, it does not always change directly into a stable element. Instead, it can go through a sequence of different unstable isotopes before reaching stability. This series of changes is known as a radioactive decay chain. Each step in the chain involves the emission of particles such as alpha (α) or beta (β), gradually changing the atomic number and mass of the nucleus.

For example, a uranium atom might decay into a thorium atom, which then decays into protactinium, and so on, until it finally becomes a stable lead isotope. The final, stable product is often known as the “end product” of the chain.

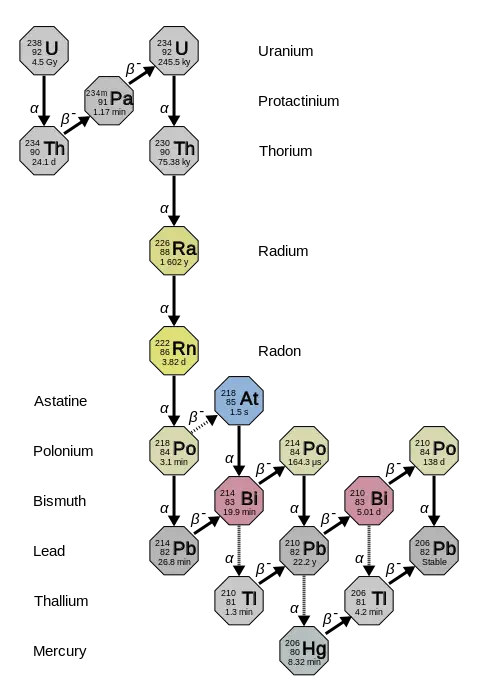
Example: Uranium-238 Decay Series

The Uranium-238 decay series is one of the most well-known decay chains. This process takes billions of years and involves a long series of alpha and beta decays, with along with gamma emissions.

The full chain looks like this:

U-238 → Th-234 → Pa-234 → U-234 → Th-230 → Ra-226 → Rn-222 → Po-218 → Pb-214 → Bi-214 → Po-214 → Pb-210 → Bi-210 → Po-210 → Pb-206 (stable)

As shown in the conceptual diagram below, each arrow represents a decay event. The alpha decay (α) reduces the atomic number by 2 and the mass number by 4. The beta decay (β) increases the atomic number by 1, leaving the mass number unchanged. The final product, Lead-206, is a stable isotope.

Radioactive Decay Chains in Physics and Medicine — Importance and Applications

Decay chains have their equal impact in theoretical nuclear physics and practical medical applications. In physics research, these chains help scientists to understand nuclear stability patterns, and predict unknown isotope properties, and study fundamental nuclear forces. The energy releases during chain decay provide insights into binding energy relationships and nuclear structure.

Medical applications rely heavily on decay chain principles. Radiopharmaceuticals often use specific chain members for targeted therapy or imaging. For example, actinium-225 deuterium chains deliver alpha particles directly to cancer cells, while technetium-99m (from molybdenum-99 deuterium) enables precise medical imaging. Understanding the behavior of daughter products ensures safe handling and effective treatment protocols.

Applications of Half-Life in Daily Life

As we have learned by now, half-life is not just a theoretical concept but a powerful and practical process through which our lives are changing. Let us discuss a few examples of how it is being used in our daily lives.

1. Medicine and Cancer Treatment

Modern nuclear medicine relies entirely on half-life principles for both diagnostic imaging and therapeutics. PET scans use fluorine-18 (half-life: 110 minutes) bound to glucose molecules, allowing doctors to assess metabolic activity in tumors. The relatively short half-life ensures minimal radiation exposure while providing clear images.

Radiotherapy applications require precise calculations of half-lives for treatment planning. Iodine-131 (half-life: 8 days) treats thyroid cancer by concentrating and delivering targeted radiation to the thyroid tissue. Doctors calculate the exact dose knowing that 93.75% of the radiation will arrive within 32 days (4 half-lives). Meanwhile, palladium-103 seeds (half-life: 17 days) implanted directly into the prostate tumor deliver concentrated radiation with minimal systemic exposure.

Medical isotope production schedules depend heavily on decay chains and half-life calculations. Technetium-99m generators use the molybdenum-99 parent (half-life: 66 hours) to continuously produce the desired imaging isotope. Hospitals receive fresh generators weekly, ensuring adequate technetium-99m availability despite the 6-hour half-life.

2. Archaeology and Dating Ancient Artifacts

Carbon-14 dating has revolutionized archaeology by providing precise age determinations for organic material up to 50,000 years old. All living things absorb carbon-14 from the atmosphere. When an organism dies, it stops taking in C-14, and the existing C-14 begins to decay with a half-life of 5,730 years.

Archaeologists measure the activity of the remaining carbon-14 and use half-life calculators to determine the ages of the samples. The famous Turin controversy centers on carbon-14 analysis showing early medieval rather than first-century dates (about 700 years old). Similarly, Ötzi the Iceman’s age of 5,300 years was confirmed by carbon-14 analysis of his preserved remains.

Advanced applications include calibration curves that account for historical atmospheric carbon-14 variations due to solar activity and nuclear weapons testing. These corrections ensure accurate dating of fossils and archaeological artifacts, making half-life calculations essential tools for understanding human history and prehistoric climate change.

3. Nuclear Energy and Waste Management

Nuclear power generation and waste management strategies depend primarily on understanding the half-lives of different isotopes. Uranium-235 (half-life: 704 million years) provides fissile material for reactor fuel, while uranium-238 (half-life: 4.47 billion years) serves as a fertile material for plutonium production.

Nuclear waste classification systems use half-life criteria to determine storage requirements. High-level waste containing isotopes with half-lives greater than 30 years requires geological storage for thousands of years. Cesium-137 and strontium-90 (both with half-lives of ~30 years) dominate the radiation levels for the first 300 years, while transuranic elements with much longer half-lives determine long-term containment strategies.

Reactor designs include half-life calculator to manage xenon poisoning. Xenon-135 (half-life: 9.2 hours) strongly absorbs neutrons, creating operational challenges during reactor startup after shutdown periods. Understanding its decay kinetics allows operators to predict when reactors can safely restart without xenon interference.

4. Space Exploration

Radioisotope thermoelectric generators (RTGs) allow deep space missions by converting the heat of radioactive decay into electricity. Plutonium-238 (half-life: 87.7 years) provides ideal properties such as high energy density, a manageable half-life for missions spanning decades, and essentially minimizing the need for alpha-day shielding.

The Voyager spacecraft, launched in 1977, are still operating today due to their plutonium-238 RTGs. After 47 years, about 65% of the original plutonium remains active, and powering instruments for the exploration of interstellar space. Mission planners calculated power budgets knowing that power output would decline over an expected 87.7-year half-life.

Mars rovers use similar principles, with the Perseverance rover’s multi-mission radioisotope thermoelectric generator designed to operate effectively for at least 14 years. Engineers sized the plutonium-238 inventory knowing that 85% would remain after the duration of that mission, providing ample power margin for extended operations.

Conclusion

Half-life is not just a scientific idea—it’s a practical tool we use to understand the past, manage energy today, and even plan for the future. Scientists use it to date ancient objects with carbon dating, and engineers rely on it to power spacecraft through radioactive decay. Nuclear physics is deeply connected to the world we live in.

Now that you understand the basics and have our easy half-life calculator, you can solve any problem related to radioactive decay with confidence. Try the calculator with different values, and then challenge yourself by taking our Nuclear Physics Quiz to test your knowledge and sharpen your skills.

Recommended Reads For Curious Minds

• Modern Physics for Scientists and Engineers by Stephen Thornton
• Introduction to Nuclear Physics by W. N. Cottingham
• Fundamentals of Radiochemistry by Jean-Pierre Adloff

FAQs on Half-Life and Radioactive Decay